In order to assess the performances of the MAX codes, we are building up a system of continuous benchmarking. Due to the complexity of the flagship codes, it is not realistic to consider benchmarks exploring all the running parameters, or the features related to all the possible simulations. For this reason, we select a number of scientific challenges, relevant in estimating the flagship code performances. These "use cases" represent our set of benchmarks, on which the progresses of the work made by MAX are evaluated.
Quantum Espresso
Most of the applications of the suite are designed for the efficient usage of the state-of-the-art HPC machines using multiple parallelization levels. The basal workload distribution can be done using MPI + OpenMP multithreading, or offloading it to GPGPUs, depending on the nodes’ architecture. This parallelization level also provides an efficient data distribution among the MPI ranks. This allows to compute systems with up to ∼ 10^4 atoms. The offloading or the usage of a growing number of MPI ranks are able to scale down the computational cost of 3D FFTs and other operations on 3D data grids.
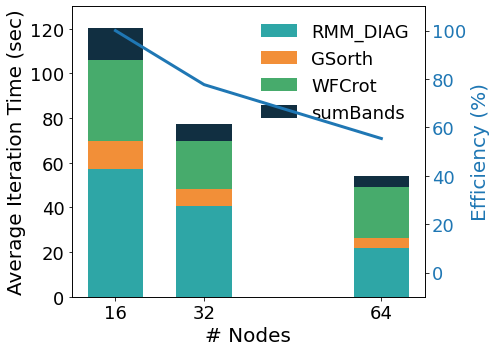
In the figure above we show the performance analysis for a mid-size case (A Carbon nanotube functionalized with two porphyrine molecules, about 1500 atoms, 8000 bands, 1 k-point) on an HPC homogeneous nodes’ cluster. The kernels distribute their workload on the lower parallelization group, except for WFCrot whose perfomance relies instead on parallel or accelerated linear algebra specific libraries. The auxiliary MPI parallelization levels allow to obtain further scaling. The band parallelization level distributes the operations on wave functions of different basal groups. The two upper parallelization levels – pools and images – are very efficient because they distribute the computations in concurrent quasi-independent blocks; as shown in the figure below for a PH calculation on 72 atoms quartz, executed on an heterogeneous nodes’ HPC cluster equipped with Ampere GPGPUs.
Siesta
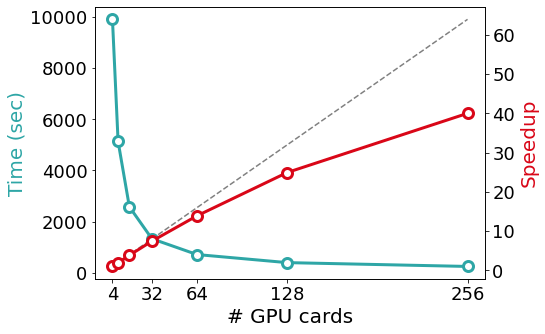
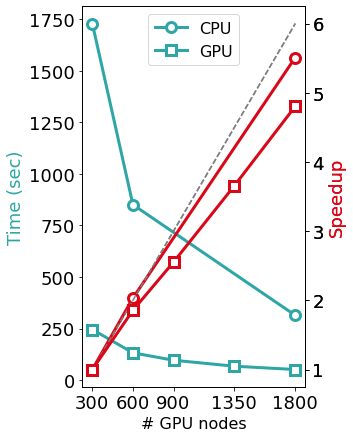
SIESTA is written in modern Fortran with both MPI and OpenMP parallelism. For most problems, the most computationally-demanding stage of SIESTA execution is the solver stage (calculation of energy eigenvalues from the above-mentioned sparse objects). On the one hand, SIESTA provides a range of solvers of its own, from cubic-scaling diagonalisation to linear-scaling methods, that exploit existing linear algebra libraries such as SCALAPACK, ELPA, and DBCSR. On the other hand, SIESTA can leverage a number of libraries that implement favourably-scaling solvers, such as CHESS (Fermi Operator Expansion method) and PEXSI (Pole EXpansion and Selected Inversion method). All these libraries are designed for parallel execution, and they are progressively incorporating support for offloading to an increasing breadth of GPU architectures. The figure below exemplifies the scaling of some of the solvers mentioned above in the Marconi 100 supercomputer: starting from the CPU version of the ELPA solver, the same solver with GPU offloading displays a significant speed-up, although with some degradation in its scaling probably due to no longer saturating the GPUs. In comparison, the (CPU-only) PEXSI solver allows for scaling to a significantly larger number of nodes with less degradation. The accuracy of the PEXSI solver improves with the number of poles used in the expansion it performs; it can be seen how the increased accuracy enables scaling to a larger number of nodes, thus not increasing the time to solution.
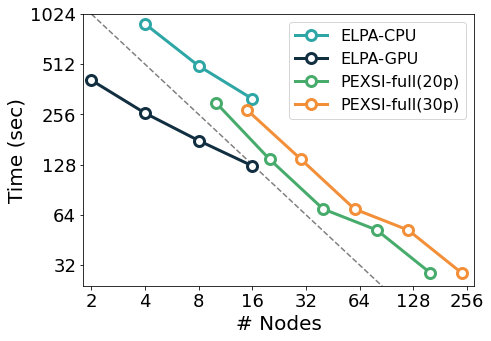
In the Figure: Time to solve the diagonalization problem corresponding to a piece of SARS-COV-2 protein surrounded by water molecules, with approximately 58,000 orbitals, in Marconi 100). The dashed line shows the ideal scalability behaviour.
Yambo
YAMBO has a user-friendly command-line interface, flexible I/O procedures, and it is parallelised by using an hybrid MPI plus OpenMP infrastructure, very well integrated with support of GPGPU-based heterogeneous architectures. This makes it possible to distribute the workload to a large number of parallel levels. In practice, depending on the kind of calculation, all the variables to be used (k/q grids, bands, quasi-particles, etc) are distributed along the different level of parallelisation. At present YAMBO has been shown to be efficient in large-scale simulations (several upto few tens of thousands MPI tasks combined with OpenMP parallelism) for most of its calculation environments.
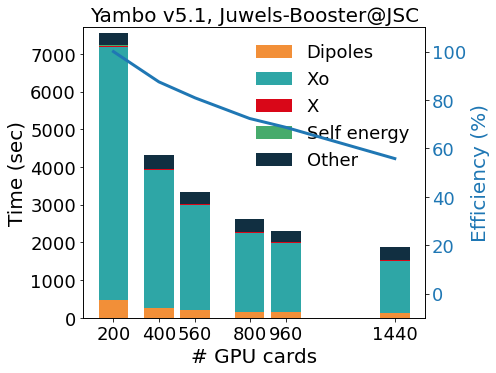
The GPU porting was first made using CUDAFortran, and more recently enlarged to other programming models (like OpenACC and OpenMP5, both in development). To avoid code duplication, we make an intense use of pre-processor macros that activate the language chosen at compile time. This allows YAMBO to optimally integrate MPIOpenMP with programming models for GPGPU. The outcome of this integration is well exemplified by the scaling tests reported in figure, for the calculation of quasi-particle corrections on a graphene/Co interface (GrCo) composed by a graphene sheet adsorbed on a Co slab 4 layers thick, and a vacuum layer as large as the Co slab. The test represents a prototype calculation, as it involves the evaluation of a response function, of the Hartree-Fock selfenergy and, finally, of the correlation part of the selfenergy. The scalability and relative efficiency are reported in the Figure as a function of the number of GPU cards and show a very good scalability up to 1440 GPUs (360 nodes on Juwels-Booster@JSC, 4 NVIDIA A100 per node).
Fleur
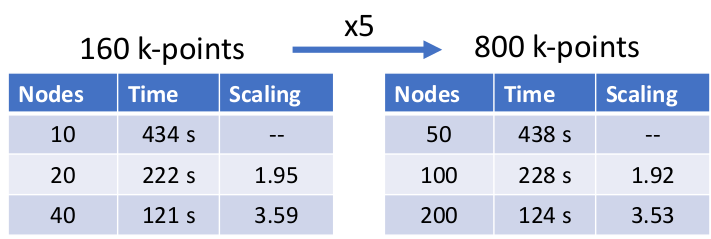
FLEUR is utilising several levels of parallelization to exploit both, intra-node and inter-node distribution of the calculation. On the most coarse level, the calculations can be split over different k-points (and q-points where present) leading to an excellent scaling behaviour. This can be seen in the following table in which we demonstrate excellent weak and good strong scalability on JUWELS booster up to roughly a quarter of the machine with
a nominal performance of approximate 15 PFlops.
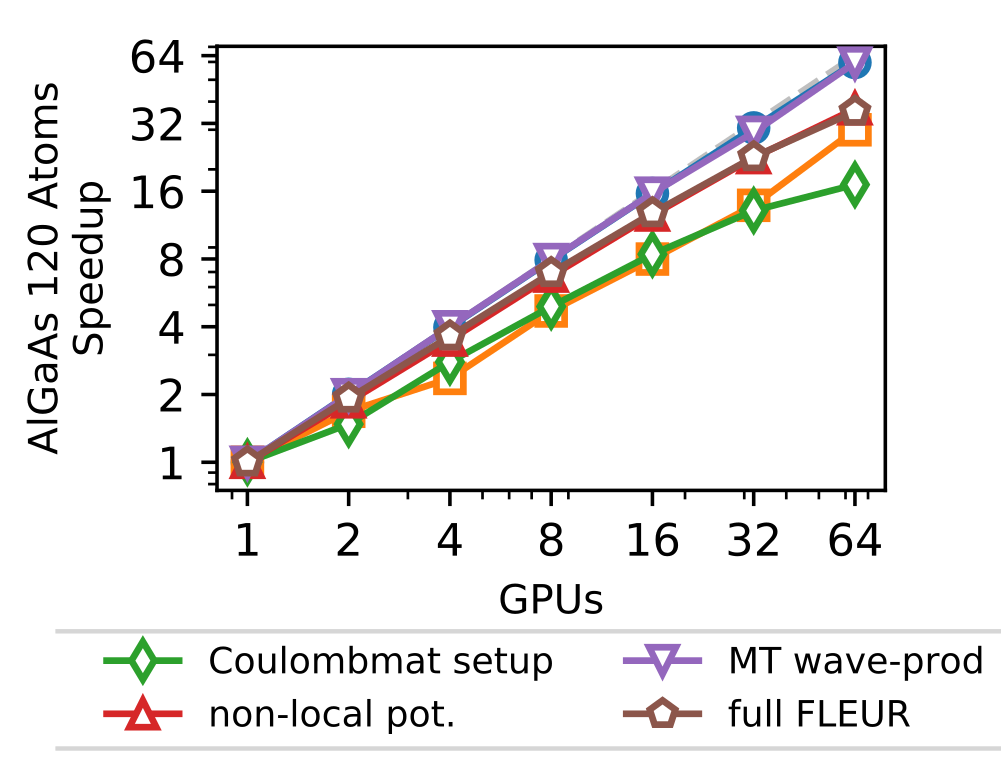
In addition to this outer parallelization level, FLEURalso employs more fine-grain parallelism, distributing the calculation associated with the different eigenstates. This parallelization is largely ’orthogonal’ to the scaling shown before in which only a single GPU was assigned to this level. This level is strongly dependent on the details of the system as well as the kernel to be used. As an example (without any outer parallelization), we show in the figure below the scalability for the calculation using hybrid functionals on the JURECA-DC cluster with 4 NVIDIA A100 cards per node, e.g. up to 16 nodes.
As a production calculation for the system studied here would require several hundred kq-points the combination of the two levels of parallelism discussed here could be scaled up to fill existing supercomputers easily.
BigDFT
BigDFT is a award-winner DFT code, recipient of the first edition (2009) of the Bull-Fourier prize for its “the ground-breaking usage of wavelets and the adaptation to hybrid architectures, combining traditional processors and graphic accelerators, leading the path for new major advancements in the domain of new materials and molecules”. It is parallelized using a combination of MPI and OpenMP and has support for GPU acceleration since the early days of GPGPU computing. Such supports involve both CUDA as well as OpenCL computing kernels, and can be routinely applied to large systems. For example, the calculation of a 12,000 atom protein system requires about 1.2 hours of wall-time on 16 nodes of the Irene-ROME supercomputer. This calculation can be further accelerated for systems composed of repeated sub-units using a fragment approach for molecules, or in the case of extended systems, a pseudo-fragment approach, both among the outcomes of MaX2 project.
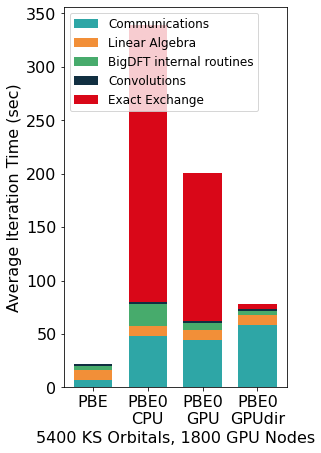
The Figure above shows the benefits induced by a multi-GPU calculation on a PBE0 calculation (seconds per 2 SCF iterations) of a system made of 5400 KS orbitals on Piz Daint. Such calculations can scale effectively up to the range of thousands of GPUs and compute nodes.
To facilitate driving the calculations of dense workflow graphs involving thousands of simulations of large systems, the code suite includes a python package called PyBigDFT as a framework for managing DFT workflows. PyBigDFT is able to handle
building complex systems or reading them from a variety of file types, performing calculations with BigDFT linked with AiiDA package, and analyzing calculation results. This makes it easy to build production analysis, thereby enabling new users’ production HPC experiences on top of the data generated from large scale DFT calculations. Currently, BigDFT is being deployed on large HPC machines including Fugaku (RIKEN, JP), Archer2 (Edinburgh, UK), and Irene-ROME (TGCC-CEA, FR).
All data in this page is updated to the MaX proposal 2022.

