Computing spectral and thermodynamic properties of correlated materials via dynamical functionals
A team of researchers proposes a novel approach for the computation of spectral and thermodynamic properties of correlated materials via dynamical functionals.
A current challenge for scientific discoveries and technological innovation is the accurate and predictive first-principles calculations of materials properties.
In recent years, Density-functional theory (DFT) has provided a major step forward in the prediction of ground-state properties. Yet, to accurately calculate spectroscopic quantities of materials remains challenging.
To overcome this limitation, research studies are implementing dynamical methods based on Green’s functions (e.g., many-body perturbation theory approaches such as GW, dynamical mean-field theory, spectral functional theories, electron-boson interaction schemes). Such methods deal with dynamical (frequency-dependent) quantities, increasing the algorithmic and numerical complexity and limiting applications.
In this study, a team of researchers proposes a new method that allows the typical operations of dynamical formulations to be analytical on a given basis, i.e., on sum over poles (SOP). Furthermore, they design a novel functional for materials science generalizing the DFT+U functional to host the dynamical screening of the crystal.
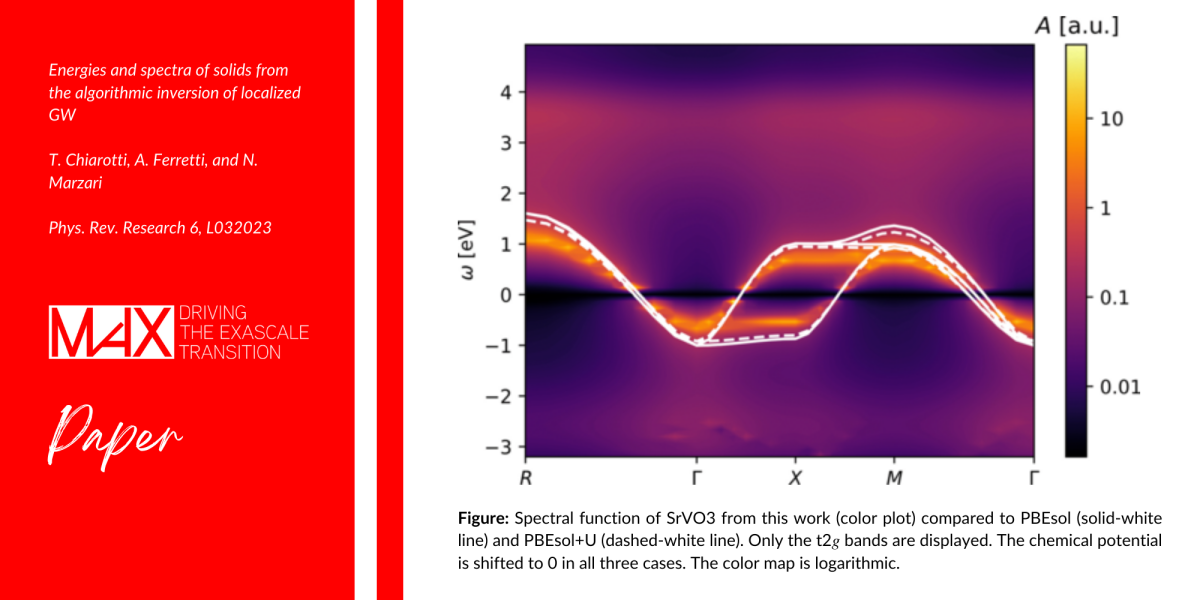
<< Our approach allows for the computation of spectral and thermodynamic properties of correlated materials via dynamical functionals. Both computational framework (algorithmic-inversion method on sum over poles) and theoretical advances (dynamical Hubbard functional) were used to obtain state-of-the-art results for SrVO3, a most discussed and paradigmatic perovskite >> explained Tommaso Chiarotti (EPFL), first author of the paper.
Researchers also prove the algorithmic efficiency of the method, and the physical accuracy of the functional, by computing the spectral, thermodynamic, and vibrational properties of SrVO3. Crucially, their results are in close agreement with experiments and state-of-the-art methods, at highly reduced computational costs and with a transparent physical interpretation.
Reference article:
Energies and spectra of solids from the algorithmic inversion of dynamical Hubbard functionals.
For those interested in the subject, check out also the companion paper:
Green's function embedding using sum-over-pole representations.



